Latin Square Design: Basic Concept, Example, Demonstration in Agri Analyze and Quiz

This blog explains Latin Square Design basics like when to use design, how to perform randomization, ANOVA structure, solved example and demonstration in Agri Analyze platform. Link of quiz is given at the end. (Reading time 15-20 mins.)

Latin Square Design (LSD)

In agricultural field experiments, fertility gradients often run parallel to one side of the field. Occasionally, these gradients run parallel to both sides and in a new field, the predominant gradient direction may be unknown. In other words, when the experimental field is divided into smaller plots (experimental units), variation can occur in one direction, two directions, or exhibit cyclic variation in the case of a new field.

In animal experiments, variation among experimental units can be influenced by characteristics such as age, growth, body weight, or lactation number. When variation is known for a single characteristic, local control can be applied by grouping experimental units into blocks or replications with similar characteristics, as seen in randomized complete block designs. This principle becomes more effective when variability in two characteristics is considered, such as fertility gradients in two directions in field experiments or variations in age and body weight in animal studies. Double grouping of experimental units based on these characteristics can significantly reduce experimental error.

The Latin square design exemplifies this principle by grouping experimental units into rows and columns. For 't' treatments, 't' experimental units are organized into 't' rows and 't' columns, ensuring each treatment appears once per row and column. This method ensures homogeneity within rows and columns based on the two characteristics considered.

This design is also effectively utilized in laboratory experiments, industrial studies and soil science research, where experimental units can be grouped based on two characteristics.

In the Latin square design, double grouping helps reduce errors due to differences among rows and columns, offering greater error reduction opportunities compared to the randomized block design. Each row and column contain every treatment, allowing differences to be attributed to soil variation. For optimal results, rows and columns should be similar in width to equally share soil heterogeneity, resulting in compact, almost square plots. Since these plots are typically small, soil variation within them is minimized. Unlike randomized designs where blocks need not be contiguous, the latin square design loses its advantages if plots are not contiguous, making it somewhat less flexible than block designs.

In an LSD, the degrees of freedom for error are given by (t-1)(t-2), where t is the number of treatments. For very small values of t the degrees of freedom for error become extremely limited, making it difficult to obtain reliable estimates of experimental error and perform valid statistical tests. With more than 10 treatments, arranging the treatments in a balanced Latin square layout becomes increasingly difficult. The physical or logistical setup of the experiment can become unwieldy, making it harder to maintain the required structure and control for row and column effects. For example for 10 treatments the number of experimental units are 100, for 11 121 and for 12 144. The number of experimental units increases disproportionately making experiment incontinent for larger treatments.

Application

When the number of treatments ranges from 5 to 10 and experimental units can be grouped according to two characteristics in field experiments, animal studies, soil science research, industrial applications and laboratory trials, the latin square design is an appropriate and effective choice.

Randomization and Layout plan

Randomization in the latin square design involves selecting a square at random from all possible Latin squares. Fisher and Yates provided complete sets of latin squares for 4 x 4 to 6 x 6 sizes and sample squares up to 12 x 12. Cochran and Cox offered sample latin squares ranging from 3 x 3 to 12 x 12. The randomization method suggested by Cochran and Cox is as follows:

For 3 x 3 squares: Assign letters to the treatments, which need not be random. Write out a 3x3 square, randomize the arrangement of the three columns and then randomize the arrangement of the last two rows.

For 4 x 4 squares: There are four distinct squares that cannot be obtained from each other by simply rearranging rows and columns. Randomly select one of these four squares and then randomly arrange all the columns.

For 5 x 5 squares: Numerous distinct squares exist that cannot be derived from one another by rearranging rows and columns. Assign letters to the treatments randomly, then randomize all the columns and rows.

The necessary conditions require treatments to be randomized so that each treatment appears exactly once in every column and row. The simplest method to achieve this is by randomly selecting a "reduced Latin square" (or a Latin square in standard form) from the 56 standard Latin squares provided in the Fisher and Yates statistical tables for 5 x 5 Latin squares. A standard Latin square is one where the first row and the first column are arranged in alphabetical order.

Procedures for randomizing treatments in LSD

Step 1: A reduced Latin square or standard square was selected randomly from the 56 Latin squares. The random number chosen was 52.

	C1	C2	C3	C4	C5
R1	A	B	C	D	E
R2	B	C	D	E	A
R3	C	D	E	A	B
R4	D	E	A	B	C
R5	E	A	B	C	D

Step 2: Randomization of rows: Random numbers 3, 2, 1, 5, 4. Arranging the rows in this order.

	C1	C2	C3	C4	C5
R3	C	D	E	A	B
R2	B	C	D	E	A
R1	A	B	C	D	E
R5	E	A	B	C	D
R4	D	E	A	B	C

Step 3: Randomization of columns: Random numbers: 3, 1, 2, 4, 5. Arranging the rows in this order we get

	C3	C1	C2	C4	C5
R3	E	C	D	A	B
R2	D	B	C	E	A
R1	C	A	B	D	E
R5	B	E	A	C	D
R4	A	D	E	B	C

Step 4: Randomization of letters or treatments: Random numbers: 2, 5, 1, 4, 3

	C3	C1	C2	C4	C5
R3	C	A	D	B	E
R2	D	E	A	C	B
R1	A	B	E	D	C
R5	E	C	B	A	D
R4	B	D	C	E	A

The treatment random numbers are used to replace A, B, C, D and E in order. The goal is to create a square such that each treatment appears exactly once in each row and column, with the treatments allocated in a completely random order. After constructing the square, the experiment will be implemented by applying treatment A to the plots corresponding to the positions of A's in the final square, treatment B to the plots corresponding to the positions of B's and so on.

The experimental area is divided into plots with the number of plots in each row and column equal to the number of treatments. Each treatment appears once per row and column, resulting in n rows, n columns and n x n plots for n treatments. The plot shape can vary from square to long strips and the Latin square itself can be square or rectangular. This design is highly reliable for 5 to 8 treatments, up to a maximum of 12 treatments.

Example of LSD with Analysis:

An experiment on cotton was conducted to study the effect of foliar application of urea combined with insecticidal sprays on cotton yield. The details of the experiment are provided below.

The treatments for the experiment are as follows:

· T1 serves as the control

· T2 involves applying 100 kg N/ha as urea, with 50% at final thinning and 50% at flowering as top dressing

· T3 includes applying 100 kg N/ha as urea, with 80 kg N/ha in four equal split doses as a spray and 20 kg/ha at final thinning

· T4 consists of applying 100 kg N/ha as CAN (Calcium Ammonium Nitrate), with 50% at final thinning and 50% at flowering as top dressing

· T5 combines T2 with six insecticidal sprays

· T6 combines T4 with six insecticidal sprays

Design layout (6 x 6)

3.10

5.95

1.75

6.40

3.85

5.30

4.80

2.70

3.30

5.95

3.70

5.40

3.00

2.95

6.70

5.95

7.75

7.10

6.40

5.80

3.80

6.55

4.80

9.40

5.20

4.85

6.60

4.60

7.00

5.00

4.25

6.65

9.30

4.95

9.30

8.40

Row/Column	C1	C2	C3	C4	C5	C6	Row total
R1	3.10	5.95	1.75	6.40	3.85	5.30	26.35
R2	4.80	2.70	3.30	5.95	3.70	5.40	25.85
R3	3.00	2.95	6.70	5.95	7.75	7.10	33.45
R4	6.40	5.80	3.80	6.55	4.80	9.40	36.75
R5	5.20	4.85	6.60	4.60	7.00	5.00	33.25
R6	4.25	6.65	9.30	4.95	9.30	8.40	42.85
Column total	26.75	28.9	31.45	34.4	36.4	10.6	198.50

Treatment SS

Treatment							Treatment Total	Treatment mean
T1	3.00	2.70	1.75	4.95	4.80	5.00	22.20	3.70
T2	4.80	2.95	3.80	4.60	3.85	8.40	28.40	4.73
T3	3.10	4.85	3.30	6.55	9.30	7.10	34.20	5.70
T4	4.25	5.80	6.60	5.95	3.70	5.30	31.60	5.27
T5	6.40	6.65	6.70	6.40	7.00	5.40	38.55	6.43
T6	5.20	5.95	9.30	5.95	7.75	9.40	43.55	7.26

Error SS

ESS = Total SS – RSS – CSS – TSS

= 128.33 – 34.44 – 21.59 – 47.21 = 25.09

Degrees of freedom calculation

Row = t – 1 = 6 – 1 = 5

Column = t – 1 = 6 – 1 = 5

Error = (t – 1) * (t-2) = 5 * 4 = 20

Total = total observation -1 = 36 – 1 = 35

Mean Square

Row MS = Row SS / Row DF = 34.44 / 5 = 6.88

Column MS = Columns SS / Column DF = 21.59 / 5 = 4.31

Treatment MS = treatment SS / error df = 47.21 / 5 = 9.44

Error MS = error SS / error df =25.09 / 20 = 1.25

Calculated F

Row = Row MS / Error MS = 6.88 / 1.25 = 5.49

Column Cal. F = Column MS / Error MS = 4.61 / 1.25 = 3.44

Treatment Cal. F = Treatment MS / Error MS = 9.44 / 1.25 = 7.52

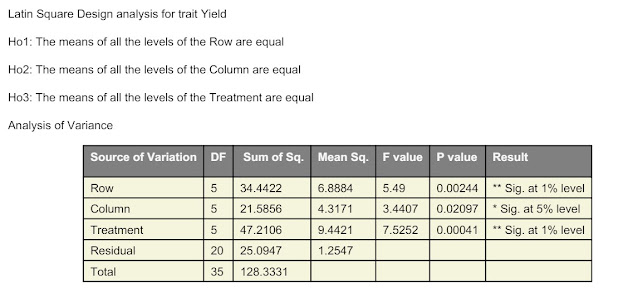
ANOVA

Source	DF	SS	MS	Cal F
Row	5	34.44	6.88	5.49
Column	5	21.59	4.31	3.44
Treatment	5	47.21	9.44	7.52
Error	20	25.09	1.25	-
Total	35	128.33	-	-

From the ANOVA results, the treatment effect was found to be significant at the 5% level of significance (Cal F. (7.52) > Tab F_{(0.05, 20)} (2.71)). Therefore, we reject the null hypothesis (H₀: all treatments are equal) and conclude that at least one pair of treatments means are to be significant. To compare treatments means, Critical difference (CD) is required.

Conclusion based critical difference

Treatment T6 (100 kg N/ha as CAN + six insecticidal sprays) resulted in a significantly higher cotton yield and was on par with T5 (100 kg N/ha as urea + six insecticidal sprays) based on critical difference. Significantly lower yield was observed with T1 (control), which was on par with T2 (100 kg N/ha applied as urea).

Steps to perform analysis of LSD in Agri Analyze

Step 1: To create a CSV file with columns for Row, Column, Treatment and Yield (Gain)

Link of the Data Set

Step 2: Go with Agri Analyze site. https://agrianalyze.com/Default.aspx

Step 3: Click on ANALYTICAL TOOL

Step 4: Click on DESIGN OF EXPERIMENT

Step 5: Click on Latin Square Design Analysis

Step 6: Select CSV file.

Step 7: Select treatment, row, column and dependent variable (e.g., Yield).

Step 8: Select a test for multiple comparisons, such as the Least Significant Difference (LSD) test, to determine significant differences among groups. Same as for Duncan’s New Multiple Range Test (DNMRT), Tukey’s HSD Test.

Step 9: After clicking on the submit button pay a nominal fee and download the report.

Snips of the output file