Estimation of Genetic Parameters in Plant Breeding: Theory, Example and Demonstration in AgriAnalyze tool
The blog is about estimation of genetic parameters like genotypic variance, phenotypic variance, heritability, genetic advance, genetic advance as a percentage of mean, phenotypic coefficient of variation (PCV), genotypic coefficient of variation (GCV) for the RCBD trails of genotypes. (Reading time 20 mins).
1.
INTRODUCTION
In a general
statistical context, a parameter
refers to a numerical characteristic or attribute that describes a population.
It can be a fixed value or an unknown quantity that helps to describe or
summarize a specific aspect of a population. Genetic Parameter
is a statistical measure that quantifies the genetic contributions to traits
within a population of an organism. Genetic parameter estimation in plant
breeding involves quantifying various genetic components that influence traits
of interest, such as yield, disease resistance or quality attributes. These
parameters provide critical insights into the genetic basis of these traits,
informing breeding decisions aimed at improving crop varieties.
Genetic parameters encompass a
range of measurements, including heritability, genetic variance and genetic
advance. Heritability indicates the proportion of phenotypic
variation in a trait that is attributable to genetic factors, guiding breeders
on the potential response to selection. Genetic variance
quantifies the variability in traits due to genetic differences among
individuals, crucial for understanding trait inheritance patterns. Genetic
advance measures the expected improvement from selection, facilitating
efficient breeding strategies. Understanding these genetic parameters empowers
plant breeders to develop improved cultivars tailored to specific agricultural
needs, enhancing crop productivity, resilience and quality. These parameters
are estimated through statistical analyses of trait data collected from
breeding experiments, utilizing methodologies such as variance component
analysis and heritability estimation. The experiments are laid in various experimental
designs that ensures valid and interpretable results through randomization,
replication and control. Designs range from simple completely randomized
designs to complex ones like randomized complete block designs (RCBD), factorial designs and Latin
squares. These designs help isolate variable effects and understand their
interactions.
1. RANDOMIZED
COMPLETE BLOCK DESIGN
Randomized
Complete Block Design (RCBD) is a fundamental experimental design used
extensively in plant breeding research to control for variability within
experimental units. In RCBD, each block contains all genotypes, with random
assignment within blocks, controlling for variability and ensuring
comprehensive genotype comparison. Hence, it is called "Randomized
Complete Block Design." This design reduces experimental error and enhances
the precision of genotype mean comparisons by accounting for block-to-block
variability. It is essential for drawing valid inferences about genotype
effects while minimizing the influence of extraneous factors.
2.1 When
RCBD is used?
The
RCBD is employed in agricultural research under specific conditions to achieve
reliable and precise results. Here are scenarios when RCBD is used: heterogeneous experimental units, known gradients, multiple genotypes, limited experimental units, small-scale
trials etc.
2.2 Assumptions
of RCBD
The
RCBD operates under several key assumptions to ensure valid and reliable
results: homogeneity within blocks,
independence of observations, additivity of effects, random assignment,
normality, equal variance, no missing data etc.
2.3 Randomization steps in RCBD
Randomization
in a Randomized Complete Block Design (RCBD) is a crucial step to ensure
unbiased allocation of treatments to experimental units within each block. Here
are the detailed steps for randomization in RCBD:
- 1. Identify the Treatments
- 2. Define the Blocks
- 3. Assign Treatments Randomly within Each Block
- 4. Record the Assignment
- 5. Repeat for All Blocks
- 6. Verify Randomization
- 7. Create a Layout Plan
2.4 Analysis
of Variance (ANOVA) for RCBD
In a RCRD, the Analysis of Variance
(ANOVA) model provides a
comparison by partitioning of variance due to various sources.
It is used to analyze the data and test the significance of genotype effects. The statistical model for ANOVA in RCBD is as
under:
Here the null hypothesis is set as all genotypes means are equal
and the alternative hypothesis is at least one genotype pair differs
significantly. Significance of the mean sum of squares due to replications (Mr)
and genotypes (Mg) is tested against error mean squares (Me). A comparison of
the calculated F (Mg/Me) with the critical value of F corresponding to genotype
degrees of freedom and error degrees of freedom gives the idea to accept or
reject the null hypothesis.
2.5 Different statistic related to RBD design
2.5.1 Standard error of mean (SEm):
2.5.2 Coefficient of Variation (CV%):
2.5.3 Critical difference at 5% level of significance
2.6 What if replication source of
variation found significant in RCBD?
2.6.1 Reasons for Significant Replication in Plant Genotype Experiments
This includes environmental micro-variation (soil heterogeneity, microclimatic conditions, etc.,), management and cultural practices (inconsistent application of treatments, differences in planting depth and spacing etc.,), biotic factors (pest and disease pressure, microbial activity etc.,), phenotypic plasticity (adaptive responses), measurement and sampling error (human error in measurement, instrument calibration etc.,)
2.6.2 Addressing Significant Replication in Plant Genotype Experiments
This can be achieved by improving experimental design (enhance block homogeneity, increase number of replicates etc.,), standardize cultural practices (consistent treatment application, uniform planting techniques etc.,), control environmental factors (monitor and manage microclimate, soil management etc.,), regular monitoring for biotic factors (pest and disease management, microbial inoculants etc.,), refine measurement techniques (training and calibration, automated measurements etc.,)
3 CALCULATION OF SIMPLE MEASURES OF VARIABILITY
Simple measures of
variability include range, standard deviation, variance, standard deviation and
coefficient of variation. These measures help in understanding the distribution
and spread of data, which are essential for statistical analysis and
interpreting the variability within a data set for given character.
3.1 Range: The difference
between the maximum and minimum values in a data set. Provides a quick sense of
the spread of the data, but is sensitive to outliers.
Range = Maximum Value - Minimum Value
3.2 Standard Deviation (SD): A
measure of the average distance of each data point from the mean. Indicates how
spread out the data points are around the mean. A smaller SD indicates data
points are close to the mean, while a larger SD indicates they are more spread
out.
Where, xi is each data point, x ̅ is the mean of the data and n is the number of data points
3.3 Variance: The
average of the squared differences from the mean. It measures the dispersion
of data points. It's the square of the standard deviation.
3.4 Coefficient of Variation (CV): The
ratio of the standard deviation to the mean, expressed as a percentage. It standardizes
the measure of variability by comparing the standard deviation relative to the
mean. Useful for comparing the degree of variation between different data sets,
especially those with different units or widely different means.
4. Variance
Components
In the context of plant breeding and genetics, ANOVA (Analysis of
Variance) is often used to partition the observed variance into different
components: phenotypic variance, genotypic variance, and environmental
variance. These components are crucial for understanding the underlying
variability and for estimating the respective coefficients of variation.
4.4 What if genotypic variance is negative?
If σ2g (genotypic variance) is negative, it indicates that the calculated value is not feasible since variance, by definition, cannot be negative. This situation typically arises due to small sample size, large experimental error, incorrect data or calculation etc. To address this issues increase replications, improve experimental design, re-evaluate data etc. In summary, a negative genotypic variance suggests the need for a reassessment of the experimental design, data quality and analysis methods.
5. COEFFICIENTS OF VARIATION
5.1 Phenotypic Coefficient of Variation (PCV): Measures the extent of phenotypic variability relative to the mean of the trait.
5.2 Genotypic Coefficient of Variation (GCV): Measures the extent of genotypic variability relative to the mean of the trait.
5.3 How to Interpret the Relative
Values of GCV, PCV and ECV?
The relative values of
Genotypic Coefficient of Variation (GCV), Phenotypic Coefficient of Variation
(PCV), and Environmental Coefficient of Variation (ECV) provide insights into
the sources and magnitude of variability within a genetic population.
- GCV is High Compared to PCV: PCV typically exceeds or equals GCV since it
includes both genetic and environmental variance. If GCV surpasses PCV,
this suggests a calculation error; review for accuracy.
- PCV is High Compared to GCV: PCV is higher than GCV, indicating
substantial environmental influence on the trait. The difference suggests
significant environmental variance. Despite genetic variability, breeders
must minimize environmental effects to select effectively based on genetic
potential.
- ECV is Higher than GCV: The trait is heavily influenced by
environmental factors, with minimal genetic variability. Phenotypic
selection may be difficult. Introducing new genetic material could help
increase genetic variability and improve selection efficiency for the
trait.
- High GCV and High PCV: This
indicates that the trait is strongly influenced by genetic factors, but
environmental factors also play a significant role. Despite the
environmental influence, the high genetic variability suggests good
potential for improvement through selection. Focus on stabilizing the
environment to harness the genetic potential effectively. Breeders can
make significant progress by selecting superior genotypes.
- High GCV and Low PCV: This
suggests that the trait is predominantly influenced by genetic factors,
with minimal environmental impact. The high genetic variability is not
masked by environmental effects. This is an ideal situation for breeders.
Selection will be highly effective since the phenotypic performance
directly reflects the genetic potential.
- Low GCV and High PCV: This
indicates that the trait is largely influenced by environmental factors,
with little genetic variability. The high phenotypic variability is mostly
due to environmental effects. Selection might be less effective due to the
low genetic variability. Breeders may need to focus on improving
environmental conditions or management practices to reduce the
environmental variance. Additionally, exploring wider genetic bases or
introducing new germplasm could be considered to increase genetic
variability.
- Low GCV and Low PCV: This suggests that the trait is relatively stable with minimal influence from both genetic and environmental factors. The lack of variability might indicate that the trait is either highly conserved or has reached a selection plateau. Limited scope for improvement through selection. Breeders might need to introduce new genetic material to increase variability. Alternatively, focus could shift to other traits with higher variability and potential for improvement.
6.
Heritability and Genetic advance
Heritability and Genetic advance are important selection parameters. Heritability estimates along with the genetic advance are normally more helpful in predicting genetic gain under selection than heritability estimates alone. However, it is not necessary that a character showing high heritability will also exhibit high genetic advance.
6.2 How to interpret the result of heritability in broad sense?1. Low
Heritability (0-30%): A low percentage of phenotypic variation in the
trait is due to genetic factors. Most of the observed variation is likely due
to environmental influences. Selective breeding for this trait might be less
effective because genetic differences contribute minimally to the trait's
expression. Instead, focus on optimizing environmental conditions to improve
the trait.
2. Moderate Heritability (30-60%): A
moderate percentage of phenotypic variation is due to genetic factors. Both
genetics and environment play significant roles in influencing the trait. Selective
breeding can lead to moderate improvements in the trait. Genetic gains can be
achieved, but it is also essential to manage environmental factors to fully
express the genetic potential.
High Heritability (60% and above): A high
percentage of phenotypic variation is due to genetic factors. Most of the
variation in the trait can be attributed to genetic differences among
individuals. Selective breeding is highly effective for this trait. Significant
genetic improvements can be made, and the trait is less influenced by
environmental factors.
6.3 Estimation of Genetic advance (GA)
Genetic advance refers to the improvement in a trait achieved through selection. It depends on the selection intensity, heritability and phenotypic standard deviation of the trait. The expected genetic advance (GA) can be calculated for each character by adopting the following formula at 5 % selection intensity using the constant ‘K’ as 2.06.
6.5 How to Interpret the Result of Genetic Advance as Per Cent of Mean?
SOLVED EXAMPLE
Dataset: The
experiment was laid in Randomized Complete Block Design with three replications
in maize (Zea mays L.) by using 30 genotypes. The data were observed
from each replication by randomly selected plants for days to 50% flowering. Link of Dataset
|
Genotypes |
Replications |
Genotype total |
Genotype mean |
||
|
R1 |
R2 |
R3 |
|||
|
G1 |
66 |
75 |
75 |
216.00 |
72.00 |
|
G2 |
68 |
75 |
76 |
219.00 |
73.00 |
|
G3 |
70 |
75 |
80 |
225.00 |
75.00 |
|
G4 |
70 |
81 |
86 |
237.00 |
79.00 |
|
G5 |
72 |
68 |
74 |
214.00 |
71.33 |
|
G6 |
66 |
72 |
80 |
218.00 |
72.67 |
|
G7 |
59 |
63 |
74 |
196.00 |
65.33 |
|
G8 |
66 |
69 |
79 |
214.00 |
71.33 |
|
G9 |
72 |
80 |
78 |
230.00 |
76.67 |
|
G10 |
64 |
66 |
83 |
213.00 |
71.00 |
|
G11 |
84 |
72 |
74 |
230.00 |
76.67 |
|
G12 |
60 |
64 |
75 |
199.00 |
66.33 |
|
G13 |
62 |
68 |
65 |
195.00 |
65.00 |
|
G14 |
63 |
72 |
75 |
210.00 |
70.00 |
|
G15 |
73 |
81 |
70 |
224.00 |
74.67 |
|
G16 |
58 |
84 |
70 |
212.00 |
70.67 |
|
G17 |
77 |
82 |
86 |
245.00 |
81.67 |
|
G18 |
64 |
69 |
75 |
208.00 |
69.33 |
|
G19 |
82 |
82 |
84 |
248.00 |
82.67 |
|
G20 |
72 |
74 |
75 |
221.00 |
73.67 |
|
G21 |
75 |
80 |
78 |
233.00 |
77.67 |
|
G22 |
70 |
76 |
82 |
228.00 |
76.00 |
|
G23 |
76 |
83 |
82 |
241.00 |
80.33 |
|
G24 |
77 |
76 |
75 |
228.00 |
76.00 |
|
G25 |
77 |
83 |
70 |
230.00 |
76.67 |
|
G26 |
76 |
84 |
86 |
246.00 |
82.00 |
|
G27 |
83 |
68 |
72 |
223.00 |
74.33 |
|
G28 |
61 |
75 |
84 |
220.00 |
73.33 |
|
G29 |
67 |
78 |
60 |
205.00 |
68.33 |
|
G30 |
67 |
70 |
78 |
215.00 |
71.67 |
|
Replication total |
2097 |
2245 |
2301 |
|
|
|
Grand total |
6643 |
||||
7.1 Analysis of Variance
Null hypothesis for genotypes and replication
H0: There are no significant differences among means of genotypes under study.
Ha: There are no significant differences among means of replications under study.
7.
STEPS TO
PERFORM ANALYSIS OF GENETIC PARAMETER ESTIMATION IN AGRI ANALYZE
Step 1: To create a CSV file with columns for Genotype, replication and trait
(DFF). Link of Dataset
Step 2: Go with Agri Analyze site. https://agrianalyze.com/Default.aspx Register by using email and mobile number
Step 3: Click on
ANALYTICAL TOOL
Step 4: Click on GENETICS
AND PLANT BREEDING
Step 5: Click on GENETIC
PARAMETER ESTIMATION

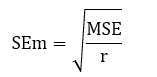


























Comments