Strip Plot Analysis with Agri Analyze: From Basics to Solved Examples

The blog contains basics of strip plot design, randomization, ANOVA model, all the formulas and solved example along with demonstration in Agri Analyze. (Reading time 15 min.)

The Strip Plot Design (SPD) is particularly suitable for two-factor experiments where higher precision is needed for measuring the interaction effect between the factors compared to measuring the main effects of either factor individually. This design is also ideal when both sets of treatments require large plots. For instance, in experiments involving spacing and ploughing treatments, cultural convenience necessitates larger plots. Ploughing strips can be arranged in one direction, and spacing strips can be laid out perpendicular to the ploughing strips. This arrangement is achieved using:

• Vertical strip plot for the first factor (the vertical factor)
• Horizontal strip plot for the second factor (the horizontal factor)
• Interaction plot for the interaction between the two factors.

The vertical and horizontal strip plots are always perpendicular to each other. However, their sizes are unrelated, unlike the main plot and subplot in the split plot design. The interaction plot is the smallest. In a strip plot design, the precision of the main effects of both factors is sacrificed to improve the precision of the interaction effect.

Randomization and Layout Planning for Strip Plot Design

Step 1: Assign horizontal plots by dividing the experimental area into r blocks, then dividing each block into horizontal strips. Follow the randomization procedure used in RBD, and randomly assign the levels of the first factor to the horizontal strips within each of the r blocks, separately and independently.

Step 2: Assign vertical plots by dividing each block into b vertical strips. Follow the randomization procedure used in RBD with b treatments and r replications, and randomly assign the b levels to the vertical strips within each block, separately and independently.

Layout Example:

A sample layout of strip-plot design with six varieties (V1, V2, V3, V4, V5 and V6) as a horizontal factor and three nitrogen rates (N1, N2 and N3) as a vertical factor in three replications.

Example of Strip Plot Design

In the previous chapter, this dataset was used for a split-plot design and now the same dataset will be used to illustrate a strip plot design.

A strip plot design was used to investigate the effects of irrigation levels (Horizontal factor) and fertilizer types (Vertical factor) on the yield of a particular crop. The experiment was conducted over four replicates (R1, R2, R3, R4).

Factors:

Horizontal Factor (A - Irrigation Levels):

A1: Low Irrigation

A2: Medium Irrigation

A3: High Irrigation

Vertical Factor (B - Fertilizer Types):

B1: Organic Fertilizer

B2: Inorganic Fertilizer

B3: Mixed Fertilizer

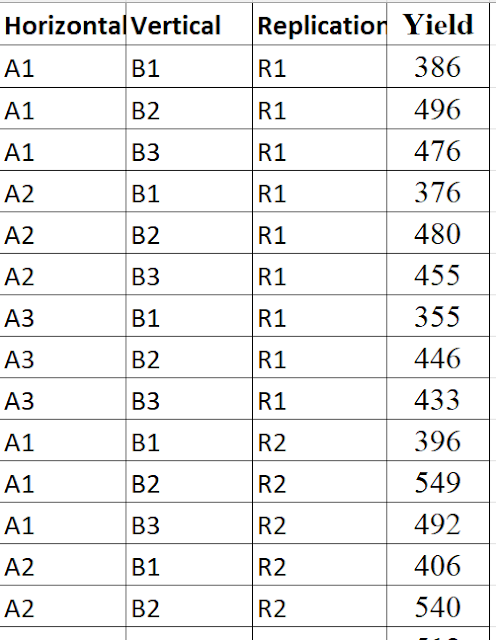
Treatments	R1	R2	R3	R4
A1B1	386	396	298	387
A1B2	496	549	469	513
A1B3	476	492	436	476
A2B1	376	406	280	347
A2B2	480	540	436	500
A2B3	455	512	398	468
A3B1	355	388	201	337
A3B2	446	533	413	482
A3B3	433	482	334	435

Final ANOVA Table for Crop Yield Analysis Using Strip Plot Design with Irrigation and Fertilizer Treatments:

					TABLE F
SV	DF	SS	MS	CAL F	5%	1%
Replication	3	61636.97	20545.66	28.12	3.49	10.80
Horizontal plot (A)	2	12391.17	6195.58	8.48	5.14	10.92
Error (A)	6	4382.61	730.44
Vertical Plot (B)	2	128866.67	64433.33	81.35	5.14	10.92
Error (B)	6	4752.44	792.07
A X B	4	304.17	76.04	0.62	3.26	5.41
Error (C)	12	1462.72	121.89
Total	35	213796.75

Calculation of degrees of freedom:

Replication DF: r-1 = 4-1=3

Main plot (A): a-1=3-1=2

Error (A): (r-1)*(a-1)=3*2=6

Main plot (B): b-1=3-1=2

Error (B): (r-1)*(b-1)=3*2=6

A x B: (a-1)*(b-1)=2*2=4

Error (C): (r-1)*(a-1)*(b-1)=3*2*2=12

Total: rab-1=4*3*3-1=35

Calculation of MS:

            Replication: 61636.97/3=20545.66

            Main plot (A): 12391.17/2=6195.58

            Error (A): 4382.61/6=730.44

            Main plot (B): 128866.67/2=64433.33

            Error (B): 4752.44/6=792.07.

            A x B: 304.17/4=76.04

            Error (C): 1462.72/12=121.89

Conclusion:

·       The calculated F-value (28.12) is much greater than the critical F-values at both 5% (3.49) and 1% (10.80) significance levels. Therefore, there is strong evidence to suggest that there are significant differences between the replicates.

·       The calculated F-value (8.48) for horizontal factor exceeds the critical F-value 5% (5.14) significance levels. This indicates that there are significant differences among the irrigation level.

·       The calculated F-value (81.35) for vertical factor exceeds the critical F-value at 1% (10.92) significance level. This indicates that there is highly significant variation among level of fertilizer.

·       The calculated F-value (0.62) for interaction between main factor and sub factor (A x B) which is less than critical F-value at 5% (2.93) significance level. This indicate that there is non-significant interaction between irrigation and fertilizer.

·       For the irrigation, highest yield was observed for A1 and A2 were found statistically at par with it based on critical difference.

·       For the fertilizer, highest yield was observed for B2 and none of the level of fertilizer at par with it based on critical difference.

·       For the interaction (A x B), highest yield was observed for A1 x B2 and none of the combination of two factor at par with it.

Steps to perform analysis of split plot design in Agri Analyze

Step 1: To create a CSV file with columns for replication, Horizontal factor (A), vertical factor (B) and Yield. Link of the dataset

Step 2: Go with Agri Analyze site https://agrianalyze.com/Default.aspx

Step 3: Click on ANALYTICAL TOOL

Step 4: Click on DESIGN OF EXPERIMENT

Step 5: Click on STRIP PLOT DESIGN ANALYSIS

Step6: Select CSV file

Step 7: Select Replication, Horizontal factor (A), Vertical factor (B) and Dependent variable (Yield)

Step 8: Select a test for multiple comparisons, such as Least Significant Difference (LSD) test or Tuckey's test or Duncan's New Multiple Range Test (DNMRT test) for grouping of treatment means.

Step 10: After submit download analysis report.

Output Result

Link of the output file

REFERENCES

Gomez, K. A., & Gomez, A. A. (1984). Statistical Procedures for Agricultural Research. John wiley & sons. 108-120.

This blog is written by:

 Darshan Kothiya

Content Writer 

Agri Analyze