Spearman Rank Correlation Analysis using Agri Analyze

-

 The blog is about Spearman Rank Correlation theory, when to use, calculation along with formulas, testing its significance, solved example and step by step guide for Agri Analyze (Reading time 10 mins) 

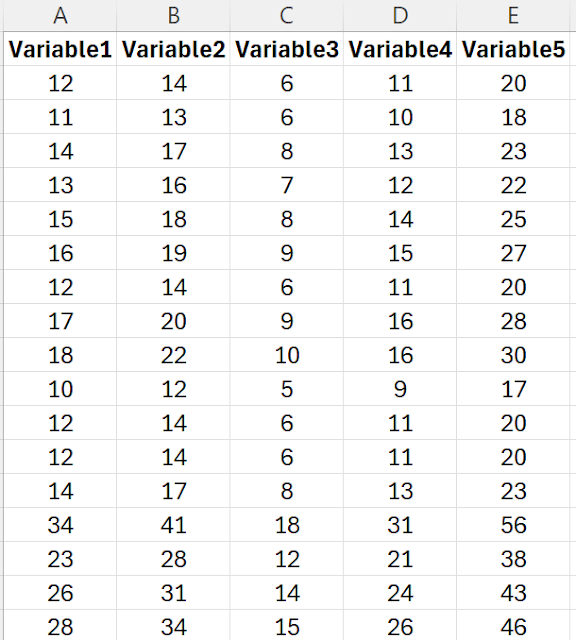
Correlation is a statistical measure that quantifies the strength and direction of the relationship between two variables. For example, it can be used to assess whether there is a connection between the heights of fathers and their sons. 

There are two primary types of correlation analysis:

  • Parametric Correlation: This method, often using Pearson's correlation coefficient (r), measures the linear relationship between numerical variables. It assumes a specific distribution of the data.
  • Non-Parametric Correlation: Employing techniques like Kendall's tau or Spearman's rho, these methods analyze the relationship between variables based on their ranks rather than their actual values. They are suitable for categorical data or ordinal (rank) data and do not require assumptions about data distribution.

One of the key assumptions in correlation analysis is that both variables being studied are normally distributed. If at least one of the variables follows a normal distribution, linear correlation can still be used. However, if neither variable is normally distributed, the linear correlation method is not appropriate. In such situations, rank correlation should be utilized instead.

There are two distinct methods for computing rank correlation: Spearman's rank correlation and Kendall's tau. Both methods can be applied to the same dataset. Numerically, Spearman's rank correlation typically yields higher values than Kendall's tau. However, both methods generally produce nearly identical inferences, so there is no compelling reason to favor one over the other. Spearman's rank correlation is more widely used due to its computational simplicity.

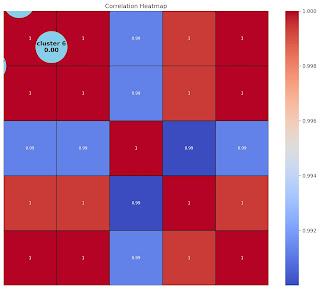
Spearman's rank correlation is sometimes called . In order to avoid confusion with the population correlation coefficient , the notation , is used to represent Spearman's correlation coefficient. Spearman's rank correlation procedure starts with ranking of the measurements of the variable X and Y separately. The differences between the ranks of each of n pairs are then found out. They are denoted by d. The Spearman's rank correlation is then computed by using the formula:



Testing the Significance of the Correlation Coefficient: A Step-by-Step Guide
To test the significance of the correlation coefficient, typically perform a hypothesis test to determine whether the observed correlation is statistically significant. The steps for testing the significance of the correlation coefficient r are as follows:

Solved example of Spearman Rank Correlation
Problem statement: There are two variables X and Y each having 5 observations. Compute the Spearman rank correlation and also test its significance using t test. The data is shared below:
X: 10, 20, 30, 40, 50  and Y: 20, 25, 15, 35, 30


Steps to perform Spearman Rank Correlation in Agri Analyze:
Dataset consists of 5 variables. Each has 18 observations. The snip of the dataset is shared below:

Step1: Go with Agri Analyze site. Direct link  
Step2: Click on ANALYTICAL TOOL followed by CORRELATION AND REGRESSION ANALYSIS followed by PEARSON CORRELATION
Step3: Upload the csv file and Click on SUBMIT button
Step4: Click on the download

Output Report:
The output will have three components 1) Heatmap 2) Correlation with p values 3) Interpretation report
1) Heatmap


2) Spearman Rank Correlation Matrix

3) Smart interpretation


Additional Topics:

The blog is written by


 
Location: Hyderabad, Telangana, India

Comments

Post a Comment

Popular posts from this blog

Estimation of Genetic Parameters in Plant Breeding: Theory, Example and Demonstration in AgriAnalyze tool

-
Image
The blog is about estimation of genetic parameters like genotypic variance, phenotypic variance, heritability, genetic advance, genetic advance as a percentage of mean, phenotypic coefficient of variation (PCV), genotypic coefficient of variation (GCV) for the RCBD trails of genotypes. (Reading time 20 mins). 1.      INTRODUCTION      In a general statistical context, a parameter refers to a numerical characteristic or attribute that describes a population. It can be a fixed value or an unknown quantity that helps to describe or summarize a specific aspect of a population. Genetic Parameter is a statistical measure that quantifies the genetic contributions to traits within a population of an organism. Genetic parameter estimation in plant breeding involves quantifying various genetic components that influence traits of interest, such as yield, disease resistance or quality attributes. These parameters provide critical insights into the genetic bas...
Read more

F test: Theory, Solved Example and Demonstration in Agri Analyze

-
Image
 The blog discuss in details about theory of F test, its use cases, solved example (manually) and a demonstration using online tool Agri Analyze (Reading time 10 min)  Introduction The F-test is a statistical method used to compare the variances of two samples or the ratio of variances across multiple samples. It assesses whether the data follow an F-distribution under the null hypothesis, assuming standard conditions for the error term (ε). The test statistic, denoted as F, is commonly used to compare fitted models to determine which best represents the underlying population. F-tests are frequently employed in models fitted using least squares. The test is named after Ronald Fisher, who introduced the concept as the "variance ratio" in the 1920s, with George W. Snedecor later naming the test in Fisher’s honor. Definition An F-test uses the F-statistic to evaluate whether the variances of two samples (or populations) are equal. The test assumes that the population follows an ...
Read more